“It’s the season to be jolly …” a famous Christmas carol starts, and this year CodinGame.com brought us programmers a present in the form of their Winter Challenge 2024. Being a nerd and a game enthusiast, tackling these kinds of problems always brings out a smile on my face 😉

The overall premise of the challenge is that you get a problem to solve programmatically, while competing against other people doing the same. The best your algorithm is, the higher you’ll rank. The competitors are divided into leagues, and as you move up the leagues the challenge becomes more complex. I’ve never considered myself an expert on these things, but nothing like a learning opportunity, so I went at it again this year.

So what the winter challenge 2024?

This year you’ll be playing the part of an organism, living on a game board. The goal is to outgrow a competing organism over 100 turns. You can grow new organs to an adjacent field. You consume proteins while growing, but can gain more by growing organs onto protein caches found on the board. If you grow more organs than you opponent, you win. Oh yeah, and the board changes between games.

Here’s an image of what the board looks like in league “Wood 3” after the first turn has elapsed.

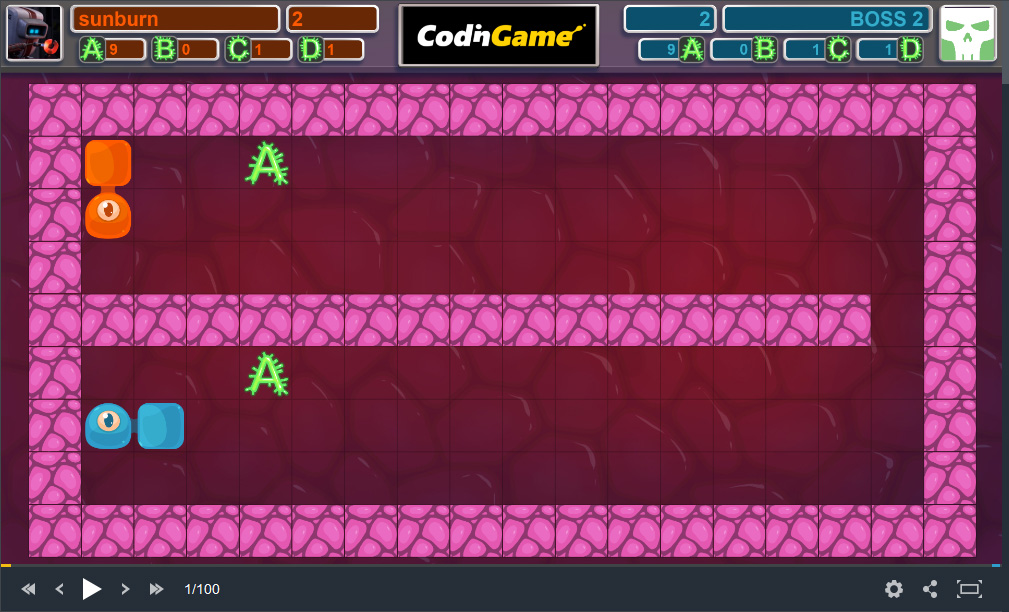
Seems simple enough, so game on!

To bold grow where no one has grown before …

Having thought about how to become the biggest organism on the board, I divided the problem it into a set of sub problems. I want my organism to:

1. Find the distance to all protein caches
2. Pick the closest cache
3. Calculate the shortest path to the protein cache
4. Grow an organ on the shortest path
5. End turn, by going back to 1.

I can treat the board as a Cartesian coordinate system and use a two dimensional table as the underlying data structure for each tile. So if this was just a flat board, calculating the distance would be fairly simple math. Unfortunately the world is full of obstacles, and unfortunately our tiny simulation of it is no exception. Someone decided to put up walls! Alas simple math will not get us there.

Back in my student years I came across something called graph theory. The short version is that we can see the board as a set of nodes (each tile). Nodes can be connected to one another by edges. In our case edges exist between two adjacent tiles, as we cannot grow diagonally. So going from one node to another is done by traveling along the edges. Having a wall represented in the graph would basically be a node with no edges connected to it, thereby preventing us from going there. Ok, this is all fine an dandy, but where does this get us you may ask. The good thing about entering into a know domain is that you get to use known ways of solving the problem. Enter graph solving algorithms 😀

The shortest path between two points

There are a number of suitable algorithms one can use, but I went for a simple approach – Djikstra’s algorithm. We wanted to know the distance to each protein cache, but Djikstra can give us the distance to each point on the board. And I foresee us needing at a later point…

My board representation would look something like this, with asterisks being walls, ‘X’ being root nodes and ‘A’ being protein caches.

* * * * * * * * * * * * * * * * * *
*                                 *
* X                               *
*         A                       *
* * * * * * * * * * * * * * * *   *
*                                 *
* X                               *
*         A                       *
* * * * * * * * * * * * * * * * * *

After having implemented the algorithm I could then run it to calculate the distance, giving me this.

-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
--  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 --
--  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 --
--  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 --
-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- 17 --
-- 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 --
-- 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 --
-- 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 --
-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

Sweet, now I just need to read the values in the table for each protein cache and pick the lowest value.

Backtracking isn’t so bad …

Djikstra’s algorithm has a really simple way of finding the shortest path. Beginning at the destination, check the distance to every connected node and pick the one with the lowest value and remember that. Repeat this for the node you just found until you reach a zero distance coordinate and voila all the nodes you remember forms the shortest path.

Time to grow

So from here I took the coordinates from the node with distance = 1 in the shortest path and grew an organ there. And with that I grew big enough to enter the next league 🙂